Professor, hoje tem aula de quê ???

 Seja bem-vindo ao Blog do Professor Sinésio R. Gomes.

Na seção " Professor, hoje tem aula de quê ??? " você encontrará artigos interessantes e material das aulas teóricas e práticas. 

A seção de informações é dividida por matérias e temas dirigidos aos alunos de cursos técnicos de Eletroeletrônica, Aprendizagem Industrial na área de Eletricista de Manutenção e Engenharia Elétrica.

Capítulo 01 - Notas de Aulas aplicadas de Eletricidade.

1. ELE 001: Aula 01 - Evolução e domínio da eletricidade;
2. ELE 002: Aula 02 - Fundamentos de eletrostática;
3. ELE 003: Aula 03 - Fundamentos de Magnetismo;
4. ELE 004: Aula 04 - Fundamentos de eletromagnetismo;
5. ELE 005: Aula 05 - Exercícios de eletricidade básica - Conceitos.
6. ELE 006: Aula 06 - Exercícios de eletricidade básica - Notação científica.
7. ELE 007: Aula 07 - Circuitos simples, série, paralelo e misto com lâmpadas.
8. ELE 008: Aula 08 - Exercícios de eletricidade básica.
9. ELE 009: Aula 09 - Tudo sobre resistores.
10. ELE 010: Aula 10 - Código de cores de resistores.
11. ELE 011: Aula 11 - Exercícios de decodificação código de resistores.
12. ELE 012: Aula 12 - Associação de resistores .
13. ELE 013: Aula 13 - Lei de Ohm, Kirchhoff e Joule .
14. ELE 014: Aula 14 - Desafio  - Lei de Ohm, Kirchhoff e Joule .
15. ELE 015: Aula 15 - Aplicação de associação de resistores (LED) .
16. ELE 016: Aula 16 - Circuitos LED's: Simples, Série e Paralelo .
17. ELE 017: Aula 17 - Divisores de tensão com resistores não lineares e "LED". 
18. ELE 018: Aula 18 - Ponte de Wheatstone com resistores não lineares e "LED". 
19. ELE 019: Aula 19 - Voltímetro de resistores e LEDs.
20. ELE 020: Aula 20 - Indicador de baterias com resistores e LEDs em série SRG.
21. ELE 021: Aula 21 - Tudo sobre Capacitores.
22. ELE 022: Aula 22 - Associação de capacitores .
23. ELE 023: Aula 23 - Carga e descarga de capacitor.
24. ELE 024: Aula 24 - Tudo sobre Indutores.
25. ELE 025: Aula 25 - Associação de indutores.
26. ELE 026: Aula 26 - Carga e descarga de indutor.
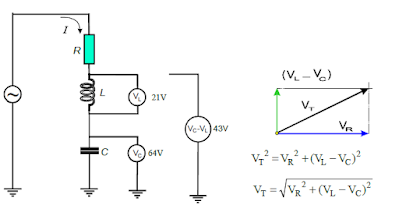
27. ELE 027: Aula 27 - Circuito RLC em série.
28. ELE 028: Aula 28 - Exercícios de Osciloscópio.
29. ELE 029: Aula 29 - Osciloscópio - Circuito RLC Série SRG.
30. ELE 030: Aula 30 - Correção do fator de potência em motores.
31. ELE 031: Aula 31 - Diagrama de motor com correção de fator de potência .

© Direitos de autor. 2018: Gomes; Sinésio Raimundo. Última atualização: 19/04/2022.

Aula 15 - Tensão e Corrente Alternada Trifásica

 Todo nosso sistema de energia elétrica residencial, comercial e industrial é alimentado por tensão e correntes alternadas. A tensão e correntes alternadas sofrem variação no passar tempo, esta alternância é natural do processo de geração da energia elétrica através de grandes geradores nas hidrelétricas e desta maneira é alternada. 

O sistema elétrico de potência é composto por equipamentos de geração, transmissão, distribuição e consumo de energia elétrica.

A geração de energia elétrica opera com tensões de 13,8 Kv.

A transmissão de energia elétrica opera com tensões de 13,8 a 500 Kv.

O sistema de distribuição de energia opera em 13,8 Kv e é aquele que se confunde com a própria topografia das cidades, ramificado ao longo de ruas e avenidas para conectar fisicamente o sistema de transmissão, ou mesmo unidades geradoras de médio e pequeno porte, aos consumidores finais da energia elétrica.

A energia distribuída, é a energia efetivamente entregue aos consumidores conectados à rede elétrica de uma determinada empresa de distribuição, podendo ser rede de tipo aérea (suportada por postes) ou de tipo subterrânea (com cabos ou fios localizados sob o solo, dentro de dutos subterrâneos). 

Assim como ocorre com o sistema de transmissão, a distribuição é também composta por fios condutores, transformadores e equipamentos diversos de medição, controle e proteção das redes elétricas. 

As redes de distribuição são compostas por linhas de alta, média e baixa tensão. Grande parte das linhas de transmissão com tensão entre 69 kV e 138 kV são de responsabilidade das empresas distribuidoras. 

Além das redes de sub transmissão, as distribuidoras operam linhas de média e baixa tensão, também chamadas de redes primária e secundária, respectivamente. As linhas de média tensão são aquelas com tensão elétrica entre 2,3 kV e 44 kV, e são compostas por três fios condutores aéreos sustentados por cruzetas de madeira em postes de concreto.

As redes de baixa tensão, com tensão elétrica que pode variar entre 110 e 440 V, são aquelas que, também afixadas nos mesmos postes de concreto que sustentam as redes de média tensão, localizam-se a uma altura inferior. As redes de baixa tensão levam energia elétrica até as residências e pequenos comércios/indústrias por meio dos chamados ramais de ligação. Os supermercados, comércios e indústrias de médio porte adquirem energia elétrica diretamente das redes de média tensão, devendo transformá-la internamente para níveis de tensão menores, sob sua responsabilidade.

Essa tensão e correntes quando geradas, primeiro crescem indo de um momento nulo ou 0 até um máximo, segundo decrescem do ponto máximo até o ponto nulo novamente, no terceiro momento elas continuam decrescendo do ponto nulo até um ponto mínimo, e por ultimo crescem do ponto mínimo até o ponto nulo encerrando o ciclo.

A corrente alternada trifásica nada mais é do que a associação de três correntes alternadas monofásicas defasadas de 120 graus elétricos, ou seja, 1/3 de período.

Diz-se que o sistema trifásico está equilibrado quando as três correntes monofásicas associadas possuem o mesmo valor eficaz e a mesma defasagem entre elas.

LIGAÇÃO ESTRELA - Esta ligação se caracteriza por possuir um ponto comum entre as três fases. Neste ponto, pode ou não ser ligado um condutor, denominado de neutro, caracterizando assim dois tipos de ligação estrela (com neutro ou sem neutro). 

No caso de motores elétricos, é utilizada a ligação estrela sem neutro, uma vez que o desequilíbrio entre as fases é, normalmente, insignificante. As relações entre as tensões e correntes de linha e fase são dadas na figura.

LIGAÇÃO TRIÂNGULO - Na ligação triangulo os três enrolamentos são ligados num circuito fechado. As relações entre as tensões e correntes de linha são dadas na figura.

O arquivo completo do sistema de distribuição trifásico pode ser baixado em: Aula 10 - Tensão e Corrente alternada Trifásica.

Aplicação de medidas e cálculos de carga trifásica está disponível em: 24_06_10 Carga Trifásica Estrela e Triângulo.

© Direitos de autor. 2016: Gomes; Sinésio Raimundo. Última atualização: 21/02/2016

Aula 14 - Potencia e correção de fator de potência em corrente alternada

A capacidade de um equipamento elétrico de produzir trabalho em um determinado tempo, a partir da energia elétrica, é chamada de potência elétrica. Em um circuito de corrente contínua, a potência é dada em watts, multiplicando-se a tensão pela corrente. No entanto, quando se trata de circuitos de CA com cargas indutivas e/ou capacitivas, ocorre uma defasagem entre tensão e corrente. Isso nos leva a considerar três tipos de potência: Potência Aparente (S), Potência Ativa (P) e Potência Reativa (Q).

Figura 01 - Potencia aparente (S)

Potência Aparente é o resultado do produto da multiplicação entre a tensão e a corrente. Em circuitos não resistivos em corrente alternada esta potência não é real, pois não considera a defasagem  que existe entre a corrente e a tensão. Recebe a notação S e é expressa em Volt Ampere (VA).

Figura 02 - Potencia ativa (P)

Potência Ativa é a potência que realmente produz o trabalho na carga. Recebe como notação a letra P e é expressa em Watts (W). No cálculo da potência ativa é importante considerar o produto entre a corrente e a tensão e também o fator de potência (cos φ).

Figura 03 - Potencia reativa (Q)

Potência reativa é a porção da potência aparente que é fornecida ao circuito. Sua função é constituir o circuito magnético nas bobinas e um campo elétrico nos capacitores. Como os campos aumentam e diminuem acompanhando a freqüência, a potência reativa varia duas vezes por período entre a fonte de corrente e o consumidor. A potência reativa aumenta a carga dos geradores, dos condutores e dos transformadores originando perdas de potência nesses elementos do circuito. A unidade de medida da potência reativa é o volt-ampère reativo (VAr) e é representada pela letra Q.

Figura 04 - Potencias em circuitos RLC

Fator de Potência se aplica quando cargas indutivas são acionadas com alimentação por corrente alternada, ocorre um fenômeno de defasagem entre as ondas da tensão e da corrente, causando o surgimento da Potência Reativa. Esta defasagem é quantificada pelo chamado Fator de Potência (FP).

Logo, de uma forma resumida,  o Fator de Potência (FP) nada mais é que uma medida de quanto da potência elétrica consumida está de fato sendo convertido em trabalho útil.

Segundo a Legislação Brasileira o Fator de Potência mínimo permitido para as contas de energia é de 0,92. Abaixo deste valor, a Concessionária deve cobrar multa na fatura de energia sobre o consumo de Potência Reativa além dos 8% máximos permitidos.

As principais cargas que causam baixo FP são lâmpadas fluorescentes, transformadores em vazio (sem carga) ou com baixa carga e motores de indução (motores mais usados na indústria). Equipamentos baseados em resistências elétricas como lâmpadas incandecentes e aquecedores elétricos em geral tem FP próximo a 1, ou seja, são os que menos contribuem para o surgimento das multas.

A forma de compensar o baixo Fator de Potência é a instalação de bancos de capacitores em paralelo na entrada de energia ou no próprio equipamento com carga indutiva. Esses bancos introduzem na instalação uma carga capacitiva, que tem o efeito contrário da carga indutiva. Isso compensa o baixo Fator de Potência e ajusta o valor para mais próximo de 1, evitando as multas.

Medidores de qualidade de energia, são importantes na identificação dos equipamentos com baixo FP e assim otimizar a implementação de projetos para correção.

O fator de potência é a razão entre a potência ativa e a potência aparente. Ele indica a eficiência do uso da energia. Um alto fator de potência indica uma eficiência alta e inversamente, um fator de potência baixo indica baixa eficiência energética. 

Um triângulo retângulo é frequentemente utilizado para representar as relações entre P (kW), Q (kvar) e S (kVA), conforme a Figura.

A energia reativa, ao sobrecarregar uma instalação elétrica, inviabiliza sua plena utilização, condicionando a instalação de novas cargas a investimentos que seriam evitados se o fator de potência apresentasse valores mais altos. O “espaço” ocupado pela energia reativa poderia ser então utilizado para o atendimento de novas cargas.

Os investimentos em ampliação das instalações estão relacionados principalmente aos transformadores e condutores necessários. O transformador a ser instalado deve atender à potência total dos equipamentos utilizados, mas devido a presença de potência reativa, a sua capacidade deve ser calculada com base na potência aparente das instalações.

Uma forma econômica e racional de se obter a energia reativa necessária para a operação adequada dos equipamentos é a instalação de capacitores próximos desses equipamentos. A instalação de capacitores porém, deve ser precedida de medidas operacionais que levem à diminuição da necessidade de energia reativa, como o desligamento de motores e outras cargas indutivas ociosas ou superdimensionadas.

A correção do fator de potência por si só já libera capacidade para instalação de novos equipamentos, sem a necessidade de investimentos em transformador ou substituição de condutores para esse fim específico.

Para iniciar um projeto de Correção do Fator de Potência deveremos seguir inicialmente duas etapas básicas:

Cálculo da Capacitância do Capacitor

1. Interpretar e analisar os parâmetros elétricos das instalações: nas Empresas em Operação, através das medições efetuadas e nas Empresas em Projeto, através dos parâmetros elétricos presumidos;

2. Ter em mãos e interpretar as especificações técnicas de todos os materiais que serão empregados na execução do projeto.

A correção pode ser feita instalando os capacitores, tendo como objetivos a conservação de energia e a relação custo/benefício. A Correção localizada é obtida instalando-se os capacitores junto ao equipamento que se pretende corrigir o fator de potência e representa, do ponto de vista técnico, a melhor solução, apresentando as seguintes vantagens: reduz as perdas energéticas em toda a instalação; diminui a carga nos circuitos de alimentação dos equipamentos; pode-se utilizar em sistema único de acionamento para a carga e o capacitor, economizando-se um equipamento de manobra; gera potência reativa somente onde é necessário. 

Quando se corrige um fator de potência de uma instalação, consegue-se um aumento de potência aparente disponível e também uma queda significativa da corrente. 

Aplicação de cálculos potência para correção de fator de potência em motores de campo distorcido está disponível em: Diagrama de motor monofásico série com correção de fator de potência e

Diagrama de motor monofásico paralelo com correção de fator de potência .

© Direitos de autor. 2024: Gomes; Sinésio Raimundo. Última atualização: 22/05/2024

Aula 13.2 - Frequência de ressonância em um circuito RLC Série

O circuito RLC é um componente fundamental de muitos dispositivos eletrônicos. É composto por três elementos:

• Resistência R;
• Indutância L;
• Capacitância C.

Em sua forma básica, todos os três elementos estão conectados em série. Outras configurações mais complicadas são possíveis e utilizadas para fins específicos. Aqui, veremos apenas o mais simples. Os circuitos RLC têm muitas aplicações. Por exemplo, você pode encontrá-los em:

• Circuitos de sintonia – conhecidos de rádios analógicos;
• Filtros – blocos básicos de equalizadores em equipamentos musicais também podem ser projetados com um circuito RC mais simples ; e
• Circuitos osciladores – convertendo sinal DC em sinal AC, por exemplo, em transmissores de rádio.

Em todas estas aplicações, a frequência de ressonância do circuito RLC é a sua principal característica. 

A frequência ressonante do circuito RLC é uma frequência natural com a qual a corrente no circuito atinge seu valor máximo e sua defasagem em relação a tensão é zero. Esta frequência natural é determinada pela capacitância C e pela indutância L.

A resistência R é responsável pelas perdas de energia presentes em todas as situações, por exemplo os motores elétricos. Já em um amplificador se tentarmos empurrar através do circuito um sinal com uma frequência diferente da natural, tal sinal será amortecido.

Você pode calcular a frequência de ressonância do circuito RLC com a seguinte equação:

• f = 1 / [2π × √(L × C)] ; onde: f - Frequência de ressonância; L – Indutância do indutor; e C – Capacitância do capacitor.

Se, por exemplo, assumirmos uma indutância L = 1 µHe a capacitância C = 2 pF, a frequência resultante é f = 112.54 MHz. Esta frequência é uma frequência típica de transmissões de rádio na faixa VHF.

O segundo número característico do circuito RLC é a qualidade conhecido como fator Q. O fator Q determina quão bom é o circuito (quanto tempo durarão as oscilações). Se o fator Q for menor que 1/2, as oscilações desaparecem rapidamente.

Ao projetar o circuito RLC, devemos ter como objetivo obter o fator Q o maior possível. A fórmula para o fator Q do circuito RLC é:

• Q = 1/R × √(L/C) ; onde: Q – Fator Q; R – Resistência; L – Indutância do indutor; e C – Capacitância do capacitor.

Para o circuito que consideramos antes com L = 1 µHe C = 2 pF, a resistência R = 1 kΩ leva ao fator Q Q = 0.7. Este valor do fator Q é bastante pequeno. Deveríamos redesenhar o circuito diminuindo a resistência ou aumentando a indutância ao custo de diminuir a capacitância (para manter a frequência natural constante). Dessa forma, obteríamos um circuito RLC melhor.

Podemos utilizar a calculadora on-line: Calculadora de frequência de ressonância

No link a seguir há exercícios de circuitos RC, RL e RLC série, onde temos que realizar os cálculos de reatância capacitiva, indutiva e impedância para definir as tensões e correntes no circuito:  19_06_02 Circuito RLC em série.

O relatório do circuito 07 - RLC série em diferentes frequências está disponível em: 24_04_07 Circuito RLC Série em F0/10, F0 e 10xF0 SRG.

© Direitos de autor. 2024: Gomes; Sinésio Raimundo. Última atualização: 01/04/2024

Aula 13.1 - Circuitos RLC séries em corrente alternada.

    Em circuitos de corrente alternada que apresentem resistências e reatâncias associadas, a oposição à passagem da corrente elétrica é denominada de impedância. Impedância é oposição total que um circuito composto por resistências e reatâncias apresenta ao fluxo da corrente elétrica. A impedância é representada pela letra Z e é expressa em ohms.

    Circuito RC série : 

Figura 01 - Circuito RC série.

O circuito RC série em corrente alternada da figura 01 (a) é um exemplo típico de circuito que contém resistência e reatância. Por esta razão o circuito RC série tem uma impedância que se opõe à passagem da corrente alternada.

    A existência de componentes reativos, que defasam correntes ou tensões, torna necessário o uso de formas particulares para o cálculo da impedância de cada tipo de circuito.

Figura 02 - Cálculo de impedância em circuito RC série.

    Tomando-se como exemplo o circuito RC série, a equação da impedância pode ser encontrada a partir da análise do gráfico fasorial das tensões mostrado na figura 01 (b). O gráfico da figura 01 (c) mostra que a resistência ôhmica do resistor e a reatância capacitiva do capacitor estão defasadas de 90º.

    A impedância do circuito RC é a soma dos efeitos de XC e R, ou seja, a soma entre o fasor XC e R.

    Graficamente, essa soma é a resultante do sistema de fasores XC e R e pode ser matematicamente calculada pelo Teorema de Pitágoras, uma vez que os fasores R, XC e Z formam um triângulo retângulo, como pode ser visto na figura 01 (c). Isolando o valor de Z, obtém-se a equação para o cálculo da impedância do circuito RC série.

• Z = √(R² + Xc²) ; onde: Z = impedância em ohms, R = resistência do resistor em ohms e XC = reatância capacitiva em ohms calculado através de XC = 1 / 2πƒC.

    Na figura 02, é apresentado um exemplo que ilustram a utilização da equação da impedância do circuito RC série.

    A corrente em um circuito RC série aplicado a uma rede de CA depende da tensão aplicada e da impedância que o circuito apresenta. Os valores de V, I e Z se relacionam segundo a Lei de Ohm, como já calculado anteriormente. Dispondo de Z, pode-se agora calcular I: se V = 100 (v) então: i = 100 / 5.379 = 0,0185 (A).

    O ângulo formado entre os fasores VR e VT (ou R e Z) é representado pela letra grega φ (lê-se fi ), se os valores de VR e VT são conhecidos (medindo-se o circuito em funcionamento), pode-se determinar o cosseno do ângulo, conforme mostrado abaixo:

• cos φ = VR/VT; onde: VR = tensão no resistor em volts, e VT = tensão do gerador.

    Conhecendo-se o cosseno de um ângulo, o seu valor pode ser determinado através de uma tabela ou de uma calculadora. 

    Da mesma forma, o ângulo φ pode ser determinado conhecendo-se os valores de R e Z, como mostrado abaixo:

• cos  φ  = R/Z; onde: R = resistência do resistor em ohms e Z = impedância em ohms.

Figura 03 - Cálculo de impedância em circuito RL série.

    Circuito RL série : A mesma sequência de cálculo é válida pra circuito com indutores mostrado na figura 04, no entanto a tensão no indutor está adiantada em 90 graus e a reatância indutiva XL é calculada através de XL = 2πƒL, como mostrado na figura 04.

• Z = √(R² + XL²) ; onde: Z = impedância em ohms, R = resistência do resistor em ohms e XL = reatância indutiva em ohms calculado através de XL = 2πƒL.

O ângulo formado entre os fasores VR e VT (ou R e Z) é representado pela letra grega φ (lê-se fi ), se os valores de VR e VT são conhecidos (medindo-se o circuito em funcionamento), pode-se determinar o cosseno do ângulo, conforme mostrado abaixo:

• cos φ = VR/VT; onde: VR = tensão no resistor em volts, e VT = tensão do gerador.

Figura 04 - Circuito RL série.

    Conhecendo-se o cosseno de um ângulo, o seu valor pode ser determinado através de uma tabela ou de uma calculadora. 

    Da mesma forma, o ângulo φ pode ser determinado conhecendo-se os valores de R e Z, como mostrado abaixo:

• cos = R/Z; onde: R = resistência do resistor em ohms e Z = impedância em ohms.

    Circuito RLC série : Um capacitor ligado em corrente alternada provoca a defasagem entre a corrente e a tensão. A tensão é atrasada 90º em relação à corrente, como ilustrado na figura 01.

Figura 05 - Circuito RLC série.

    Um indutor ligado em CA também provoca uma defasagem entre tensão e corrente. A tensão é adiantada 90º em relação a corrente, como mostrado na figura 04. Comparando os gráficos fasoriais do capacitor e do indutor, verifica-se que os efeitos são simétricos entre si. Em relação à corrente, o capacitor atrasa a tensão e o indutor adianta. Esta oposição entre os efeitos faz com que os circuitos formados por um resistor, um indutor e um capacitor ligados em série tenham um comportamento particular em CA. Este comportamento pode ser estudado tomando-se como referência o circuito RLC série mostrado na figura 05 (A).

A impedância Z do circuito RLC série é calculada da seguinte maneira:

• Z = √(R² + ( XL - Xc)² ; onde: Z = impedância em ohms, R = resistência do resistor em ohms, XL = reatância indutiva em ohms calculado através de XL = 2πƒL e XC = reatância capacitiva em ohms calculado através de XC = 1 / 2πƒC.

Já o ângulo de defasagem entre a corrente e a tensão pode ser calculado com a fórmula abaixo:

• φ = arc tang (XL−XC) / R ;  onde: R = resistência do resistor em ohms, XL = reatância indutiva em ohms calculado através de XL = 2πƒL e XC = reatância capacitiva em ohms calculado através de XC = 1 / 2πƒC.

Figura 06 - Tensões no circuito RLC série.

    Como o circuito é série, a corrente elétrica é tomada como referência, por ser única em todo o circuito. 

• A corrente circulante provoca uma queda de tensão no resistor (VR = I x R) que está em fase com a corrente, como ilustrado na figura 05 (B). 
• A corrente provoca também uma queda de tensão no indutor (VL = I x XL). A queda de tensão no indutor está 90º adiantada em relação à corrente, como ilustrado na figura 05 (B). 
• Da mesma forma, ocorre uma queda de tensão no capacitor (VC = I x XC). A queda de tensão no capacitor está 90º atrasada em relação à corrente, como pode ser visto na figura 05 (B). 

    No circuito RLC série existe uma única corrente (I) e três tensões envolvidas (VR, VL e VC), conforme mostram os gráficos senoidal e fasorial da figura 06. 

Figura 07 - Impedância no circuito RLC série.

    Desses gráficos, observa-se que a tensão no indutor e no capacitor estão em oposição de fases. As tensões VL e VC em oposição de fase atuam uma contra a outra, subtraindo-se. Esta subtração entre VL e VC pode ser observada na prática, medindo-se os valores de VC e VL isoladamente e depois medindo-se o valor VC – VL, como ilustrado na Fig.9.

Com base na subtração entre VL e VC, o sistema de três fasores (VR, VL e VC) pode ser reduzido para dois fasores : (VC – VL) e VR ou (VL – VC) e VR. Esse comportamento pode ser visto na figura 06.

    A partir do sistema de dois fasores defasados entre si de 90º, a tensão total VT pode ser determinada pelo Teorema de Pitágoras. Note que nesta equação, os termos VL e VC devem ser colocados sempre na ordem: maior menos o menor (VL – VC ou VC – VL), de acordo com a situação. Isto é importante no momento em que for necessário isolar um dos termos (VL ou VC) na equação. Observe que (VL - VC) foi tratado com um único termo para o dimensionamento da equação.

Figura 08 - Cálculo de impedância, corrente
e tensão em circuito RLC série.

    A equação para determinar a impedância de um circuito RLC série pode ser encontrada a partir de um estudo do seu diagrama fasorial e está mostrado na figura 07. Dividindo-se cada um dos fasores VL , VR e VC pela corrente I, tem-se: 

• XL = VL / I ; onde  XL = reatância indutiva em ohms calculado através de XL = 2πƒL.
• R =  VR / I ; onde R = resistência do resistor em ohms ;
• XC = VC / I ; XC = reatância capacitiva em ohms calculado através de XC = 1 / 2πƒC

A corrente no circuito RLC série depende da tensão aplicada e da impedância do circuito, conforme estabelece a Lei de Ohm para circuitos de corrente alternada:

• I = VT / Z ; onde Z = √(R² + (XL - XC)²) ; onde: Z = impedância em ohms, R = resistência do resistor em ohms, XL = reatância indutiva em ohms calculado através de XL = 2πƒL e XC = reatância capacitiva em ohms calculado através de XC = 1 / 2πƒC.

    Na na figura 08 é mostrado um exemplo que ilustra a utilização das equações da tensão total e da corrente no circuito RLC série. 

    No link a seguir há exercícios de circuitos RC, RL e RLC série, onde temos que realizar os cálculos de reatância capacitiva, indutiva e impedância para definir as tensões e correntes no circuito:  19_06_02 Circuito RLC em série.

    O relatório do circuito 03 - RLC série está disponível em: 24_04_03 Circuito RLC Série SRG.

© Direitos de autor. 2019: Gomes; Sinésio Raimundo. Última atualização: 01/04/2019

Aula 13 - Impedância e reatância de resistores, capacitores e indutores

Impedância
A impedância é a resistência (ou oposição) de um circuito à corrente alternada e sua unidade de medida é o "ohm". Para calculá-la, deve-se conhecer o valor de todos os resistores e a impedância de todos indutores e capacitores do circuito.
A impedância é representada pela letra Z e é medida em Ohms (Ω). É possível medir esse valor em qualquer circuito elétrico ou componente, e o resultado indicará qual a resistência que ele oferece ao fluxo de elétrons (corrente elétrica). Existem dois efeitos diferentes que reduzem a passagem de corrente, e ambos contribuem para a impedância.

1. A resistência (R) é a redução da passagem de corrente devido ao material e formato do componente. Esse valor é maior em resistores, mas todos componentes têm uma resistência mínima.
2. A reatância (X) é a redução da passagem de corrente causada por campos elétricos e magnéticos que se opõem às mudanças da corrente elétrica ou tensão. Esses valores são mais significantes em capacitores e indutores.

Resistor em corrente alternada

Figura 01 - Resistor em corrente alternada.

A resistência é um conceito fundamental no estudo da eletricidade, frequentemente encontrada na Lei de Ohm: V = I * R.
Essa equação permite o cálculo de qualquer uma de suas variáveis, caso as outras duas sejam conhecidas.
Para calcular resistência (R), por exemplo, escreva a fórmula como R = V / I, onde R é a resistência, medida em Ohms (Ω).
Além disso, é possível medir a resistência de um componente facilmente com auxílio de um multímetro. V é a tensão, medida em Volts (V).
Ela também é conhecida como "diferença de potencial". I é a corrente, medida em Ampères (A). R é a resistência, medida em Ohms (Ω).
O comportamento de um resistor em corrente alternada é o mesmo que em corrente contínua, ele funciona como um elemento dissipador, que converte energia elétrica em calor. Seu funcionamento é independente da direção da corrente elétrica e da frequência. Assim, dizemos que a impedância à corrente alternada (CA) de uma resistência é a mesma que a resistência à corrente contínua (DC). Isso pressupõe, no entanto, que, no caso de CA, os valores eficazes (rms) ou valores efetivos de corrente e tensão estão sendo usados.
Observe na figura 01 que a corrente e tensão estão sincronizadas quando representadas no gráfico de tensão e corrente por tempo e sobrepostas no diagrama de fase. O valor eficaz da tensão e corrente é calculado dividindo o valor de pico (Vm) por raiz quadrada de 2.

Reatância
A reatância existe somente em circuitos AC (corrente alternada) e, assim como a resistência, sua unidade de medida é o Ohm (Ω). Existem dois tipos de reatância, provenientes de componentes eletrônicos diferentes:

1. A reatância capacitiva XC é produzida por capacitores, que são componentes capazes de armazenar cargas elétricas. Conforme o fluxo de corrente em um circuito AC muda de direção, o capacitor carrega e descarrega energia repetidamente. Quanto mais tempo ele tem para carregar, maior é a oposição à corrente. Por causa disso, quanto mais rápida a mudança de fase, menor a reatância capacitiva.
2. A reatância indutiva XL é produzida por indutores, também conhecidos como bobinas ou reatores. Esses componentes criam um campo magnético que se opõem às mudanças de fase em um circuito AC. Quanto mais rápida a mudança, maior a reatância indutiva.

Capacitor em corrente alternada

Figura 02 - Capacitor em corrente alternada.

Reatância capacitiva é similar à fórmula da reatância indutiva, exceto pelo fato de que a reatância capacitiva é inversamente proporcional à frequência. 

Portanto, reatância capacitiva XC = 1 / 2πƒC, onde C é a capacitância do capacitor, medida em Farads (F). É possível medir a capacitância usando um multímetro e cálculos simples.
Se você estiver familiarizado com o "círculo unitário", imagine uma corrente AC representada dessa forma, na qual uma rotação completa de 2π radianos corresponde a 1 ciclo. Ao multiplicá-lo por ƒ, medido em Hertz (unidades por segundo), o resultado será em radianos por segundo. Este é o valor da velocidade angular do circuito, representada pela letra ômega minúscula (ω). Alguns autores escrevem a fórmula da reatância capacitiva como XC = 1/ωC.
Uma das aplicações de  capacitor em corrente alternada é para auxiliar a partida de motores monofásicos, ele é responsável para gerar um corrente elétrica em fase diferente da disponível na rede de distribuição elétrica.
O comportamento de um capacitor em corrente alternada (CA) varia sua impedância inversamente proporcional á frequência. A tensão através de um capacitor é atrasada 90 graus em relação à corrente, pois a corrente elétrica estará carregando o capacitor e a tensão é proporcional à carga gerada entre as placas do capacitor.
Observe na figura 02 que a tensão é representada deslocada 90 graus á frente da corrente no diagrama de fase.

Indutor em corrente alternada

Figura 03 - Indutor em corrente alternada.

A reatância indutiva em um circuito aumenta de acordo com a taxa de mudança de direção da corrente, também conhecida como a frequência do circuito. A frequência é representada pelo símbolo ƒ e sua unidade de medida é o Hertz (Hz). 

A fórmula completa para o cálculo da reatância indutiva é XL = 2πƒL, onde L é a indutância, medida em Henries (H).
A indutância L depende das características do indutor, como o número de espiras da bobina. Além disso, também é possível medi-la diretamente.
Se você estiver familiarizado com o "círculo unitário", imagine uma corrente AC representada dessa forma, na qual uma rotação completa de 2π radianos corresponde a 1 ciclo. Ao multiplicá-lo por ƒ, medido em Hertz (unidades por segundo), o resultado será em radianos por segundo. Este é o valor da velocidade angular do circuito, representada pela letra ômega minúscula (ω). Alguns autores escrevem a fórmula da reatância indutiva como XL=ωL.
O comportamento de um indutor em corrente alternada (CA) varia sua impedância diretamente proporcional á frequência. A tensão através de um indutor está à frente da corrente, pois o comportamento do indutor segue a lei de Lenz, resistindo ao acúmulo da corrente e atrasando essa voltagem imposta para que a corrente atinja seu valor máximo .
Observe na figura 03 que a tensão é representada deslocada 90 graus atrás da corrente no diagrama de fase.
No link a seguir há exercícios de circuitos RC, RL e RLC série, onde temos que realizar os cálculos de reatância capacitiva, indutiva e impedância para definir as tensões e correntes no circuito:  19_06_02 Circuito RLC em série.

© Direitos de autor. 2019: Gomes; Sinésio Raimundo. Última atualização: 01/04/2019

Aula 12 - Tensão elétrica contínua e alternada

Para diagnosticar o comportamento de uma instalação elétrica é necessário medir os seus parâmetros elétricos, relacioná-los, analisar os seus resultados e depois tomar decisões para a sua manutenção ou executar novas ampliações. O reconhecimento e medição dos principais parâmetros elétricos, o uso de instrumentos para medi-los e as fórmulas que os relacionam são importantes para esta atividade. Com estes fundamentos, o eletricista estará em condições de medir a tensão, corrente, resistência, potência e energia em circuitos elétricos.
TENSÃO ELÉTRICA - Definimos a tensão elétrica como a força capaz de produzir um fluxo de elétrons.
UNIDADES DA TENSÃO ELÉTRICA - A unidade da tensão elétrica é o volt, cujo símbolo é “V”. No entanto, é comum utilizar o múltiplo kV (quilovolt) e o submúltiplo mV (milivolt). Conversão: 1 kV = 1 000 V e 1 V = 1 000 mV

Figura 1.1 e 1.2

A tensão elétrica contínua (CC) é aquela na qual a sua polaridade não muda com o tempo. Figura 1.1 Tensão elétrica contínua.
A tensão elétrica alternada (CA) é aquela na qual a sua polaridade muda com o tempo e a sua magnitude é variável. Figura 1.1 Tensão alternada.

TENSÃO ELÉTRICA CONTÍNUA

Figura 2.1 - Bateria elementar

Uma bateria é um gerador de corrente contínua. A figura 2.1 mostra o interior de uma bateria elementar, constituída de eletrólito, de placas e de terminais.

A bateria é basicamente construída por dois tipos de metais mergulhados em um preparado químico, que reage com eles retirando elétrons de um e levando os para o outro.

Um dos metais, a barra de cobre, fica com o potencial elétrico positivo e o outro, o zinco, fica com o potencial elétrico negativo. Cria-se, então, uma diferença de potencial elétrico, a chamada tensão elétrica. 

A bateria tem dois terminais: um terminal chamado de polo positivo, que é marcado com o sinal +; e um terminal chamado de polo negativo, que é marcado com o sinal –.

Os elétrons ficam agrupados em maior número no polo negativo da bateria. O polo positivo, por sua vez, contém uma quantidade menor de elétrons. Esses polos nunca se alteram, portanto, a polaridade das pilhas é sempre invariável.

TENSÃO ELÉTRICA ALTERNADA

Figura 3.1 - Gerador AC

A figura 3.1 é uma representação esquemática de um gerador de corrente alternada elementar, que consiste em uma espira disposta de tal forma que pode ser girada em um campo magnético estacionário. Dessa forma, o condutor da espira corta as linhas do campo eletromagnético, produzindo a força eletromotriz (fem).

Para fornecer a tensão em CA, um gerador é composto pelos polos do ímã, pelo condutor e pelo sistema de transferência de energia. Na figura os condutores estão próximos do ímã, fazendo com que haja a máxima tensão.

Se o condutor continuar girando no campo magnético com velocidade uniforme, outros ciclos serão produzidos. O número de ciclos produzidos em uma unidade de tempo é chamado de frequência (f).

O período (T) de uma tensão, ou corrente alternada, é o tempo necessário para completar um ciclo. Ele é o inverso da frequência e a sua unidade é s (segundos).

A fórmula para o cálculo do período é: T = 1 / f ; Sendo que: T é o período em segundos (s) e f é a frequência em hertz (Hz).

A frequência é expressa em uma unidade chamada hertz (Hz), que corresponde a um ciclo por segundo (c/s).

MEDIÇÃO DA TENSÃO ELÉTRICA - O instrumento que mede a tensão elétrica é o voltímetro e conecta-se em paralelo.

Figura 4.1: Medição de tensão elétrica contínua.

MEDIÇÃO DA TENSÃO ELÉTRICA CONTÍNUA - Se você tiver um multímetro (instrumento de várias funções, entre elas o voltímetro), siga este procedimento:
1. Gire o comutador seletor à função “tensão elétrica contínua”.
2. Gire o comutador seletor à escala de tensão elétrica contínua mais alta. Você pode escolher uma escala menor se conhece o valor aproximado da tensão elétrica. Se o instrumento é do tipo autoajuste, não considere este passo.
3. Conecte a ponta de prova preta ao borne negativo (- ou COM) da bateria e a ponta de prova vermelha ao terminal positivo da bateria, como mostrado na figura 1.4.
4. Leia o valor indicado na tela do multímetro digital.

MEDIÇÃO DA TENSÃO ELÉTRICA ALTERNADA - Se você tiver um multímetro (instrumento de várias funções, entre elas o voltímetro), siga este procedimento:

Figura 4.2: Medição de tensão elétrica alternada.

1. Gire o comutador seletor à função “tensão elétrica alternada”.
2. Gire o comutador seletor à escala de tensão elétrica alternada mais alta. Você pode escolher uma escala menor se conhece o valor aproximado da tensão elétrica. Se o instrumento for do tipo autoajuste, não considere este passo.
3. Conecte as pontas de prova dos terminais do instrumento “COM” e “V" aos terminais da fonte alternada a medir, como mostrado na figura 1.5.
4. Leia o valor indicado do voltímetro analógico ou a tela do multímetro digital.

© Direitos de autor. 2019: Gomes; Sinésio Raimundo. Última atualização: 21/01/2019

Aula 11 - Galvanômetro e suas aplicações

 1.1 - Galvanômetro

O galvanômetro é um dispositivo utilizado, pela sua sensibilidade, para detectar e medir correntes elétricas (contínuas) de pequena intensidade e entra, como componente, nos amperímetros, usados para medir correntes elétricas mais intensas, e voltímetros, usados para medir diferenças de potencial elétrico.

O galvanômetro também funciona aproveitando o torque sobre uma bobina numa região de campo magnético. Um ponteiro P é montado fixo a uma bobina B que, por sua vez, é montada de modo a poder girar em torno de um eixo horizontal numa região de campo magnético gerado por um imã permanente em forma de U. Uma mola M, em espiral, exerce sobre a bobina um torque que equilibra o torque devido ao campo magnético. O vetor torque devido ao campo magnético é paralelo ao eixo de rotação da bobina e tem módulo e sentido que dependem, respectivamente, da intensidade e do sentido da corrente que circula na bobina, que é a corrente que se procura detectar ou medir.
O deslocamento da agulha é proporcional à corrente que circula pelo circuito do galvanômetro, de modo que pode ser feita uma analogia entre a posição da agulha e a intensidade da corrente. Por este motivo, esse tipo de instrumento é denominado análogo ou analógico. Uma outra característica importante desse tipo de indicador, dada pela sua forma de indicação analógica, é que a agulha se desloca de forma constante pela escala, de modo a não haver saltos de indicação.
O galvanômetro é um dispositivo utilizado para medir correntes elétricas de pequena intensidade. Além disso é o componente dos amperímetros e voltímetros reais. Quando o galvanômetro é associado a um resistor em série (multiplicativo) esse funciona como voltímetro. Quando o galvanômetro é associado a um resistor em paralelo (shunt) esse funciona como um amperímetro.
1.1.1 - Construção de Voltímetro com Galvanômetro

O Voltímetro é um instrumento destinado a medir diferença de potencial elétrico (ddp). Ele deve se ligado em paralelo com o elemento de circuito cuja ddp se quer medir.
No esquema abaixo, o voltímetro mede a ddp entre os terminais do resistor de resistência R. Para que o voltímetro não altere o valor da ddp a ser medida, sua resistência elétrica interna RV deve ser muito alta. Voltímetro ideal: resistência RV infinitamente grande (RV → ∞).
Um voltímetro é construído pela associação em série de um resistor RS com um galvanômetro. A diferença de potencial total UV aplicada sobre a associação se divide entre o resistor e o galvanômetro na razão direta de suas resistências RS e RG.

A tensão UG aplicada sobre os terminais do galvanômetro é apenas uma fração da tensão total UV aplicada sobre a associação; se soubermos em que proporção UV se divide entre UG e US poderemos determinar quanto vale a tensão total UV medindo a parte dela que atua sobre o galvanômetro.
UV = UR + UG;
Mas: iv = ir = ig ;
Asim temos:  UV = UG (1 + RS / RG);
A partir dessa relação podemos calcular o valor da resistência necessário para converter o galvanômetro num voltímetro na escala desejada.
1.1.2 - Construção de Amperímetro com Galvanômetro

O galvanômetro pode ser modificado de modo a medir correntes de intensidades maiores e nesse caso é chamado de amperímetro. Essa modificação consiste em colocar em paralelo com o galvanômetro G (Fig.1) um resistor de pequena resistência denominado shunt. Se tivermos um instrumento que possua um fundo de escala de 1 mA, por exemplo, e desejarmos medir correntes até 100 mA, poderemos usar um shunt (RS) que desvie 99 mA da corrente.
No amperímetro entra uma corrente de intensidade i (100 mA) que se divide em duas partes: uma corrente de intensidade iG ( 1 mA) que passa pelo galvanômetro (cuja resistência é RG) e uma corrente de intensidade iS ( 99 mA) que passa pelo shunt (cuja resistência é RS). Como o galvanômetro e o shunt estão em paralelo e portanto estão submetidos à mesma tensão.

U =  RG x iG = RS x iS ;
Mas: i = iG + iS ;
Asim temos  i  =  i = iG (1 + RG / RS);
O Amperímetro é um instrumento destinado a medir intensidade de corrente. Ele deve ser ligado em série com o elemento de circuito cuja corrente se quer medir.
No esquema abaixo, o amperímetro mede a intensidade da corrente que percorre o resistor de resistência R. Para que o amperímetro não altere o valor da intensidade da corrente a ser medida, sua resistência elétrica interna RA deve ser muito baixa. O Amperímetro ideal posui resistência RA nula (RA = 0).
1.1.3 - Construção de Multimetro com Galvanômetro

Dos instrumentos analógicos usados em um multímetro o ohmímetro é o único que precisa  ser energizado. No circuito acima para cada valor de corrente existe um único valor de Rx , relacionados pela equação:
Para calcular o valor de E e de R precisamos montar duas equações  relacionando as duas variáveis. Uma equação  é obtida  impondo que para  RX = 0  a corrente no instrumento será igual à de fim de escala IGM. Fazer  RX = 0  é a  operação  chamada de zerar o ohmímetro, e deve ser feita obrigatoriamente toda vez que o ohmímetro for ser usado  ou quando da mudança de escala . Observe que fazer isto significa estabelecer  o zero. Na prática, o ajuste do zero é feito através de um potenciômetro no  painel do multímetro.
A equação resultante para essa condição é:  E = ( R + RiG ).IGM     nesta equação são conhecidos  RiG e IGM, devemos portanto escrever outra equação relacionando entre si  E e R. Esta  outra equação é obtida  impondo-se que, quando RX  for igual à um determinado valor que chamaremos de resistência de meio de escala ( RDME ) a corrente no  circuito será igual a  IGM / 2, isto é, o ponteiro para no meio da escala. A equação para essa condição é:  E = ( R + RiG + RDME  ).IGM / 2.

Essas duas equações  constituem um sistema de duas equações e duas incógnitas, podendo ser resolvida facilmente. A outra marca importante corresponde à condição de   circuito aberto  RX infinita . Observe  que a escala de resistência é o contrário da escala de corrente, e mais  a polaridade da bateria interna é o contrário da polaridade indicada externamente, isso se deve à necessidade de se usar o mesmo Galvanômetro para medir corrente, tensão e resistência.
1.2 - Multímetro experimental
Este instrumento mede resistências elétricas, mede tensões contínuas e alternadas até 100 volts além de servir também como testador de continuidade na escala de resistências entre muitas outras aplicações.
A comutação é feita por bornes onde são inseridas as pontas de prova. As resistências são todas de 1/8 de watt e o microamperímetro é de 0-200 microampéres O condensador de 100nf é de poliéster com uma tensão mínima de 100 volts. As resistências variáveis servem de ajuste para cada uma das escalas. Para usar o aparelho em escala de ohms basta apenas ajustar o potenciômetro que está em série com a resistência de 4.7k e a pilha de 1.5 volts, colocar as pontas de prova entre o comum e ohm e ajustar até o ponteiro indicar zero antes de cada medida. O ajuste de cada escala de tensão pode ser obtido por comparação de outro multímetro.
© Direitos de autor. 2015: Gomes; Sinésio Raimundo. Última atualização: 26/02/2015