Aula 13.1 - Circuitos RLC séries em corrente alternada.

    Em circuitos de corrente alternada que apresentem resistências e reatâncias associadas, a oposição à passagem da corrente elétrica é denominada de impedância. Impedância é oposição total que um circuito composto por resistências e reatâncias apresenta ao fluxo da corrente elétrica. A impedância é representada pela letra Z e é expressa em ohms.

    Circuito RC série : 

Figura 01 - Circuito RC série.

O circuito RC série em corrente alternada da figura 01 (a) é um exemplo típico de circuito que contém resistência e reatância. Por esta razão o circuito RC série tem uma impedância que se opõe à passagem da corrente alternada.

    A existência de componentes reativos, que defasam correntes ou tensões, torna necessário o uso de formas particulares para o cálculo da impedância de cada tipo de circuito.

Figura 02 - Cálculo de impedância em circuito RC série.

    Tomando-se como exemplo o circuito RC série, a equação da impedância pode ser encontrada a partir da análise do gráfico fasorial das tensões mostrado na figura 01 (b). O gráfico da figura 01 (c) mostra que a resistência ôhmica do resistor e a reatância capacitiva do capacitor estão defasadas de 90º.

    A impedância do circuito RC é a soma dos efeitos de XC e R, ou seja, a soma entre o fasor XC e R.

    Graficamente, essa soma é a resultante do sistema de fasores XC e R e pode ser matematicamente calculada pelo Teorema de Pitágoras, uma vez que os fasores R, XC e Z formam um triângulo retângulo, como pode ser visto na figura 01 (c). Isolando o valor de Z, obtém-se a equação para o cálculo da impedância do circuito RC série.

• Z = √(R² + Xc²) ; onde: Z = impedância em ohms, R = resistência do resistor em ohms e XC = reatância capacitiva em ohms calculado através de XC = 1 / 2πƒC.

    Na figura 02, é apresentado um exemplo que ilustram a utilização da equação da impedância do circuito RC série.

    A corrente em um circuito RC série aplicado a uma rede de CA depende da tensão aplicada e da impedância que o circuito apresenta. Os valores de V, I e Z se relacionam segundo a Lei de Ohm, como já calculado anteriormente. Dispondo de Z, pode-se agora calcular I: se V = 100 (v) então: i = 100 / 5.379 = 0,0185 (A).

    O ângulo formado entre os fasores VR e VT (ou R e Z) é representado pela letra grega φ (lê-se fi ), se os valores de VR e VT são conhecidos (medindo-se o circuito em funcionamento), pode-se determinar o cosseno do ângulo, conforme mostrado abaixo:

• cos φ = VR/VT; onde: VR = tensão no resistor em volts, e VT = tensão do gerador.

    Conhecendo-se o cosseno de um ângulo, o seu valor pode ser determinado através de uma tabela ou de uma calculadora. 

    Da mesma forma, o ângulo φ pode ser determinado conhecendo-se os valores de R e Z, como mostrado abaixo:

• cos  φ  = R/Z; onde: R = resistência do resistor em ohms e Z = impedância em ohms.

Figura 03 - Cálculo de impedância em circuito RL série.

    Circuito RL série : A mesma sequência de cálculo é válida pra circuito com indutores mostrado na figura 04, no entanto a tensão no indutor está adiantada em 90 graus e a reatância indutiva XL é calculada através de XL = 2πƒL, como mostrado na figura 04.

• Z = √(R² + XL²) ; onde: Z = impedância em ohms, R = resistência do resistor em ohms e XL = reatância indutiva em ohms calculado através de XL = 2πƒL.

O ângulo formado entre os fasores VR e VT (ou R e Z) é representado pela letra grega φ (lê-se fi ), se os valores de VR e VT são conhecidos (medindo-se o circuito em funcionamento), pode-se determinar o cosseno do ângulo, conforme mostrado abaixo:

• cos φ = VR/VT; onde: VR = tensão no resistor em volts, e VT = tensão do gerador.

Figura 04 - Circuito RL série.

    Conhecendo-se o cosseno de um ângulo, o seu valor pode ser determinado através de uma tabela ou de uma calculadora. 

    Da mesma forma, o ângulo φ pode ser determinado conhecendo-se os valores de R e Z, como mostrado abaixo:

• cos = R/Z; onde: R = resistência do resistor em ohms e Z = impedância em ohms.

    Circuito RLC série : Um capacitor ligado em corrente alternada provoca a defasagem entre a corrente e a tensão. A tensão é atrasada 90º em relação à corrente, como ilustrado na figura 01.

Figura 05 - Circuito RLC série.

    Um indutor ligado em CA também provoca uma defasagem entre tensão e corrente. A tensão é adiantada 90º em relação a corrente, como mostrado na figura 04. Comparando os gráficos fasoriais do capacitor e do indutor, verifica-se que os efeitos são simétricos entre si. Em relação à corrente, o capacitor atrasa a tensão e o indutor adianta. Esta oposição entre os efeitos faz com que os circuitos formados por um resistor, um indutor e um capacitor ligados em série tenham um comportamento particular em CA. Este comportamento pode ser estudado tomando-se como referência o circuito RLC série mostrado na figura 05 (A).

A impedância Z do circuito RLC série é calculada da seguinte maneira:

• Z = √(R² + ( XL - Xc)² ; onde: Z = impedância em ohms, R = resistência do resistor em ohms, XL = reatância indutiva em ohms calculado através de XL = 2πƒL e XC = reatância capacitiva em ohms calculado através de XC = 1 / 2πƒC.

Já o ângulo de defasagem entre a corrente e a tensão pode ser calculado com a fórmula abaixo:

• φ = arc tang (XL−XC) / R ;  onde: R = resistência do resistor em ohms, XL = reatância indutiva em ohms calculado através de XL = 2πƒL e XC = reatância capacitiva em ohms calculado através de XC = 1 / 2πƒC.

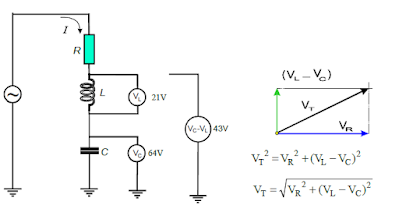Figura 06 - Tensões no circuito RLC série.

    Como o circuito é série, a corrente elétrica é tomada como referência, por ser única em todo o circuito. 

• A corrente circulante provoca uma queda de tensão no resistor (VR = I x R) que está em fase com a corrente, como ilustrado na figura 05 (B). 
• A corrente provoca também uma queda de tensão no indutor (VL = I x XL). A queda de tensão no indutor está 90º adiantada em relação à corrente, como ilustrado na figura 05 (B). 
• Da mesma forma, ocorre uma queda de tensão no capacitor (VC = I x XC). A queda de tensão no capacitor está 90º atrasada em relação à corrente, como pode ser visto na figura 05 (B). 

    No circuito RLC série existe uma única corrente (I) e três tensões envolvidas (VR, VL e VC), conforme mostram os gráficos senoidal e fasorial da figura 06. 

Figura 07 - Impedância no circuito RLC série.

    Desses gráficos, observa-se que a tensão no indutor e no capacitor estão em oposição de fases. As tensões VL e VC em oposição de fase atuam uma contra a outra, subtraindo-se. Esta subtração entre VL e VC pode ser observada na prática, medindo-se os valores de VC e VL isoladamente e depois medindo-se o valor VC – VL, como ilustrado na Fig.9.

Com base na subtração entre VL e VC, o sistema de três fasores (VR, VL e VC) pode ser reduzido para dois fasores : (VC – VL) e VR ou (VL – VC) e VR. Esse comportamento pode ser visto na figura 06.

    A partir do sistema de dois fasores defasados entre si de 90º, a tensão total VT pode ser determinada pelo Teorema de Pitágoras. Note que nesta equação, os termos VL e VC devem ser colocados sempre na ordem: maior menos o menor (VL – VC ou VC – VL), de acordo com a situação. Isto é importante no momento em que for necessário isolar um dos termos (VL ou VC) na equação. Observe que (VL - VC) foi tratado com um único termo para o dimensionamento da equação.

Figura 08 - Cálculo de impedância, corrente
e tensão em circuito RLC série.

    A equação para determinar a impedância de um circuito RLC série pode ser encontrada a partir de um estudo do seu diagrama fasorial e está mostrado na figura 07. Dividindo-se cada um dos fasores VL , VR e VC pela corrente I, tem-se: 

• XL = VL / I ; onde  XL = reatância indutiva em ohms calculado através de XL = 2πƒL.
• R =  VR / I ; onde R = resistência do resistor em ohms ;
• XC = VC / I ; XC = reatância capacitiva em ohms calculado através de XC = 1 / 2πƒC

A corrente no circuito RLC série depende da tensão aplicada e da impedância do circuito, conforme estabelece a Lei de Ohm para circuitos de corrente alternada:

• I = VT / Z ; onde Z = √(R² + (XL - XC)²) ; onde: Z = impedância em ohms, R = resistência do resistor em ohms, XL = reatância indutiva em ohms calculado através de XL = 2πƒL e XC = reatância capacitiva em ohms calculado através de XC = 1 / 2πƒC.

    Na na figura 08 é mostrado um exemplo que ilustra a utilização das equações da tensão total e da corrente no circuito RLC série. 

    No link a seguir há exercícios de circuitos RC, RL e RLC série, onde temos que realizar os cálculos de reatância capacitiva, indutiva e impedância para definir as tensões e correntes no circuito:  19_06_02 Circuito RLC em série.

    O relatório do circuito 03 - RLC série está disponível em: 24_04_03 Circuito RLC Série SRG.

© Direitos de autor. 2019: Gomes; Sinésio Raimundo. Última atualização: 01/04/2019