Aula 24 - Resistores Variáveis

 Existem dois tipos de resistores variáveis. Um deles é o resistor variável cujo valor é mudado facilmente, como o ajuste do volume do rádio.

A outra é o resistor semifixo que não se destina a ser ajustado por qualquer pessoa, mas um técnico. É usado para ajustar o estado de funcionamento do circuito pelo técnico. Resistores semifixo são utilizados para compensar as imprecisões dos resistores, e para ajustar um circuito. O ângulo de rotação da resistência variável é geralmente de cerca de 300 graus. Estes são chamados de "Potenciômetros" ou "Trimmer".

Veja na foto a resistência variável normalmente usado para controles de volume (no canto direito). O seu valor é muito fácil de ajustar. As quatro resistências no centro da foto é do tipo semifixo. Estes são montados na placa de circuito impresso. As duas resistências na esquerda são os potenciómetros aparador. Este símbolo é usado para indicar uma resistência variável em um diagrama elétrico.

Há três maneiras em que o valor de um resistor variável pode mudar de acordo com o ângulo de rotação de seu eixo. O tipo "A" ao girar no sentido horário, as mudanças de resistência alteram de  valor lentamente e, em seguida, na segunda metade de seu eixo, sua resitência muda muito rapidamente. A resistência variável tipo "A" é normalmente utilizado para o controlo do volume de um rádio, por exemplo. É bem adequado para ajustar os som baixos sutilmente, no entanto o ouvido não é tão sensível a pequenas alterações nos sons altos. A maior mudança é necessária dado que o volume é aumentado.
Já o tipo "B", a rotação do eixo e a mudança do valor da resistência estão diretamente relacionados. A taxa de variação é a mesma, linear, ao longo do variação da linha central. Este tipo serve um ajuste do valor da resistência de um circuito. Eles são muitas vezes chamados de "lineares".
Tipo "C" muda maneira exatamente oposta ao tipo "A". Nas fases iniciais da rotação do eixo, as mudanças de valor de resistência mudam rapidamente, e na segunda metade, a alteração ocorre mais lentamente. Este tipo não é muito usado.

Resistores variáveis possuem um código de 3 dígitos na sua configuração mais comum. Nesse código, os dois primeiros números representam os dois primeiros dígitos da resistência. O terceiro dígito significa o fator de multiplicação ou número de zeros que deve ser acrescentado. No caso do código 103. Ficamos então com 10 000 Ω ou 10 k Ω. A tolerância é indicado pelas letras: J - 5%, K - 10%, M - 20%, P - 25% e N - 30%.

Potenciômetro: é um componente eletrônico que possui resistência elétrica variável. Geralmente, é um resistor de três terminais onde a conexão central é deslizante e manipulável. Se todos os três terminais são usados, ele atua como um divisor de tensão. Existem comercialmente, potenciômetros confeccionados com substrato em fio e carvão condutivo, o que limita a corrente elétrica que circula nestes.

Há potenciômetros cujo giro é de 270 graus e outros de maior precisão chamados multivoltas.

Em relação à curva de resposta em função do ângulo de giro do eixo, existem dois tipos de potenciómetros, os lineares (sufixo B ao final do código) e os logarítmicos (sufixo A ao final do código comercial do valor).Exemplo de especificação de potenciômetro linear: 50 kB, ou seja, de 50.000 ohms, linear.

Os potenciômetros lineares possuem curva de variação de resistência constante (linear) em relação ao ângulo de giro do eixo. Os potenciômetros logarítmicos, por sua vez, apresentam uma variação de resistência ao ângulo de giro do eixo mais adaptada à curva de resposta de audibilidade do ouvido humano. Considerando um aparelho de som, os potenciometros lineares são recomendados para uso em controle de tonalidade (graves, médios e agudos) já os logarítmicos são mais recomendados para controles de volume.

Trimpots: estes resistores semi fixos são versões em miniatura do resistor variável. Eles são projetados para ser montado diretamente na placa de circuito e ajustado apenas quando o circuito é construído.

Por exemplo, para definir a frequência de um tom de alarme ou a sensibilidade de um circuito sensível à luz. Uma pequena chave de fenda ou ferramenta similar é necessário para ajustar as predefinições.Os Trimpots são muito mais baratos do que os potenciômetros (resistores variáveis) ​​por isso que eles às vezes são usados ​​em projetos onde um resistor variável poderia ser normalmente usado. Trimpots Multivoltas são usados ​​onde ajustes muito precisos devem ser feitas. O parafuso deve ser rodado várias vezes (10 +) para mover o cursor de uma extremidade da pista para a outra, proporcionando um controle muito fino. O Trimpots não se destina a ser ajustado por qualquer pessoa, mas um técnico. É usado para ajustar o estado de funcionamento do circuito pelo técnico. Eles são utilizados para compensar as imprecisões dos resistores, e para ajustar um circuito. O ângulo de rotação da resistência variável é geralmente de cerca de 300 graus. Alguns resistores variáveis ​​devem ser girados várias vezes para usar toda a gama de resistência que eles oferecem. Isto permite ajustes muito precisos de valor. Estes são chamados de "Trimpot" ou "Potenciômetros Trimmer". A resistência da fotografia é do tipo semifixo (Trimpot). Estes são montados na placa de circuito impresso e são os do tipo multi voltas.

Informações sobre Resistores Variáveis podem ser obtidas no link: 21_04_01 Resistor variável.

Aula 23 - Resistores e Diodo Emissor de Luz

Se você conectar um LED á alimentação de 5 volts diretamente, você irá queimá-lo instantaneamente. A alta corrente destruiria a junção pn. Para isso não ocorrer usamos um resistor limitador de corrente. Um LED vermelho usualmente trabalha com corrente direta máxima (IF) de 20 mA e tensão direta de VF: 2,0 Volt. Se quiser usá-lo onde a fonte de alimentação é de 5 Volt, temos que usar um resistor para dissipar os 3 volts restantes. Para calcular o resistor, usamos: R = V / I = (5 Volt - 2 volt) / 20 mA = 150 Ohm.
Para o resistor não queimar por excesso de calor, temos que calcular a dissipação de energia. Esta se calcula como: P = V * I =  (5 Volt - 2 volt) x 20 mA = 3 volts * 20 mA = 70 mW. Portanto, é seguro escolher um resistor de 150 Ohm com potência de 1/4 Watt (3 vezes mais potente o resistor irá trabalhar frio).
A tabela abaixo mostra as várias intensidades de corrente para diferentes cores de LED's de 5 milímetros. Usando a equação anterior com o correspondente LED que você deve ser capaz de calcular o valor da resistência necessária.
Objetivo: Medir tensão e corrente, calcular potência em resistores. Efetuar medidas com o multímetro, aprendendo a manuseá-lo de forma cuidadosa e correta.

Atividade Prática 01 : Fazer  medidas de tensão e corrente em resistores associados em série com LED's utilizando multímetro, com os valores da leitura calcular a potência dissipada e medir a temperatura do componente e fazer as anotações em tabela.

No link a seguir há exercícios de aplicação: 23_05_06 Aplicação de associação de resistores (LED)  e o relatório esperado da atividade: 24_04_06 R4 Circuitos LED's: Simples, Série e Paralelo .

© Direitos de autor. 2004: Gomes; Sinésio Raimundo. Última atualização: 23/05/2023

Aula 22 - Divisor de tensão com resistores

Nesta atividade iremos interpretar e aplicar a lei de Ohm em um circuito e montar o circuito em matriz de contatos (protoboards), obedecendo às recomendações na montagem dos componentes. Iremos também calcular as tensões em cada elemento do circuito, calcular as correntes em cada ramo do circuito e calcular a potência dissipada no resistores. Simular o circuito utilizando software, medindo as correntes e tensões em cada elemento resistivo do circuito. E por fim montar o circuito no protoboard. Medir as tensões sobre cada elemento do circuito e medir a corrente no ramo do resistor R2. Comparar os valores medidos e calculados. 

Figura 01 - Divisor de tensão com duas resistências em série.

Teoria: Ao conjunto de n resistências associadas em série dá-se o nome de divisor de tensão. Num circuito divisor de tensão, determina-se a queda de tensão ora numa ora noutra resistência, queda essa, que é uma fracção da tensão total aplicada. Supondo que a uma associação em série de duas resistências se aplica uma tensão V, a tensão existente entre os terminais de cada elemento é dado pela fórmula da figura 01. 
O divisor de tensão aplica-se somente quando se conhece a tensão Vin e Vout nos terminais de uma associação em série de resistências.
Prática: Monte o circuito com as duas resistências acima, calcule e utilize o multímetro para medir a tensão V0. Compare o valor esperado com o valor prático. Dados Vi = 12 V, R1 = 1000R, R2 = 470R.

 

No link a seguir há exercícios de aplicação: 19_03_02 Aplicação de associação de resistores (LED) 

© Direitos de autor. 2019: Gomes; Sinésio Raimundo. Última atualização: 01/04/2019
. 

Aula 21 - Leis de Kirchhoff - Malhas e Nós

Figura 01 - Definição de nó e malha.

As Leis de Kirchhoff são utilizadas para encontrar as intensidades das correntes em circuitos elétricos que não podem ser reduzidos a circuitos simples. Constituídas por um conjunto de regras, elas foram concebidas em 1845 pelo físico alemão Gustav Robert Kirchhoff (1824-1887), quando ele era estudante na Universidade de Königsberg.

Lei dos Nós
A 1ª Lei de Kirchhoff é chamada de Lei dos Nós, que se aplica aos pontos do circuito onde a corrente elétrica se divide. Ou seja, nos pontos de conexão entre três ou mais condutores (nós).

Figura 02 - Corrente elétrica na malha.

A Lei dos Nós, também chamada de primeira lei de Kirchhoff, indica que a soma das correntes que chegam em um nó é igual a soma das correntes que saem: i1 + i2 = i3 + 14.

Esta lei é consequência da conservação da carga elétrica, cuja soma algébrica das cargas existentes em um sistema fechado permanece constante.

Lei das Malhas

Já a 2ª Lei é chamada de Lei das Malhas, sendo aplicada aos caminhos fechados de um circuito, os quais são chamados de malhas.

Figura 03 - Tensão elétrica na malha.

A Lei das Malhas é uma consequência da conservação da energia. Ela indica que quando percorremos uma malha em um dado sentido, a soma algébrica das diferenças de potencial (ddp ou tensão) é igual a zero: 

Vs + VR1 + VR2 + VR3 + Vr4 = 0 .

Para aplicar a Lei das Malhas, devemos convencionar o sentido que iremos percorrer o circuito.

A tensão poderá ser positiva ou negativa, de acordo com o sentido que arbitramos para a corrente e para percorrer o circuito.

Para isso, vamos considerar que o valor da ddp em um resistor é dado por R . i, sendo positivo se o sentido da corrente for o mesmo do sentido do percurso, e negativo se for no sentido contrário.

Para o gerador (fem) e receptor (fcem) utiliza-se o sinal de entrada no sentido que adotamos para a malha.

Para aplicar as Leis de Kirchhoff devemos seguir os seguintes passos:

Figura 04 - Corrente elétrica e tensão na malha.

1º Passo: Definir o sentido da corrente em cada ramo e escolher o sentido em que iremos percorrer as malhas do circuito. Essas definições são arbitrárias, contudo, devemos analisar o circuito para escolher de forma coerente esses sentidos.

2º Passo: Escrever as equações relativas a Lei dos Nós e Lei das Malhas.

3º Passo: Juntar as equações obtidas pela Lei dos Nós e das Malhas em um sistema de equações e calcular os valores desconhecidos. O número de equações do sistema deve ser igual ao número de incógnitas.

Ao resolver o sistema, encontraremos todas as correntes que percorrem os diferentes ramos do circuito.

Se algum dos valores encontrados for negativo, significa que a sentido da corrente escolhido para o ramo tem, na verdade, sentido contrário.

No circuito abaixo, determine as intensidades das correntes em todos os ramos.

Primeiro, vamos definir um sentido arbitrário para as correntes e também o sentido que iremos seguir na malha. Neste exemplo, escolhemos o sentido conforme esquema da figura 05.

O próximo passo é escrever um sistema com as equações estabelecidas usando a Lei dos Nós e das Malhas. Sendo assim, temos:

:

Por fim, vamos resolver o sistema. Começando substituindo i3 por i1 - i2 nas demais equações:

Resolvendo o sistema por soma, temos:

Agora vamos encontrar o valor de i1, substituindo na segunda equação o valor encontrado para i2:

Finalmente, vamos substituir esses valores encontrados na primeira equação, para encontrar o valor de i1:

Resolvendo i3, temos:

Assim, os valores das correntes que percorrem o circuito são: 3A, 8A e 5A.

No link a seguir há exercícios de aplicação: 19_03_03 Lei de Ohm, Kirchhoff e Joule .

No link a seguir há exercícios para montagem em laboratório: 23_03_03 Lei de Ohm, Kirchhoff e Joule e sua solução para o circuito simples, circuito série, circuito paralelo e circuito misto.

© Direitos de autor. 2019: Gomes; Sinésio Raimundo. Última atualização: 30/04/2021

Aula 20 - Associação Mista de Resistores

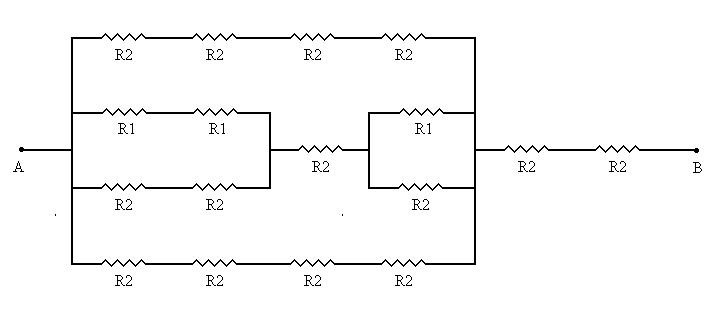
 No caso da associação mista, temos um combinado dos dois tipos de associação de resistores, série e paralelo. Para determinar a resistência equivalente, devemos começar pelas malhas independentes, ou seja, aquelas cujo resultado não dependa das outras malhas do circuito. Veja como proceder num circuito como o da figura 01.  

Para o exemplo irei utilizar todos os resistores iguais  a 100 Ω.

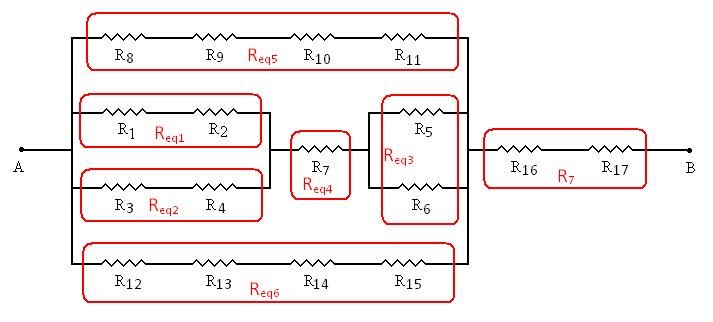Aparentemente, é um circuito complexo. Mas separamos os trechos independentes de malha, circulando-os em vermelho e renomeando os resistores equivalente, também em vermelho. É o que mostra a Figura 02. Note que no meio do circuito, temos basicamente uma linha de corrente que obrigatoriamente passa pelo resistor R₇.

Para cálculo devemos notar que há cinco associações em série R_eq1, R_eq2, R_eq5, R_req6 e R_req7, que é calculado com a soma simples dos resistores e uma em paralelo R_eq3 que é calculado com a soma dos inversos dos valores dos resistores.

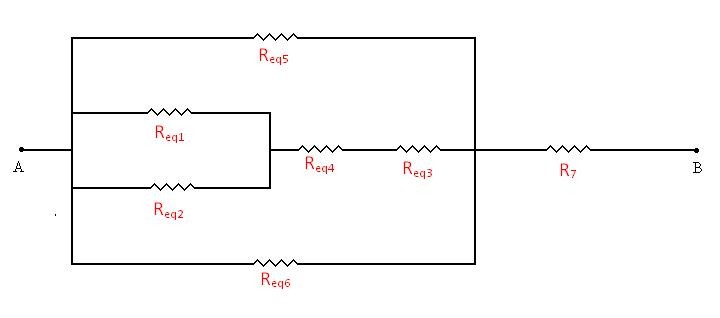Note que o circuito apresenta cinco trechos independentes, em série. São eles R_eq1, R_eq2, R_eq4, R_req6 e Rr₇. R_eq3 é o único trecho independente em paralelo.  Após os cálculos da resistência equivalente em cada trecho, teremos um “novo circuito”, igual ao da Figura 03.

Após os cálculos teremos: R_eq1 = 200 Ω, R_eq2 = 200 Ω, R_eq5 = 400 Ω, R_eq6 = 400 Ω e R_eq7 = 200 Ω. Já R_eq3 = 50 Ω e R_eq4 = 100 Ω.

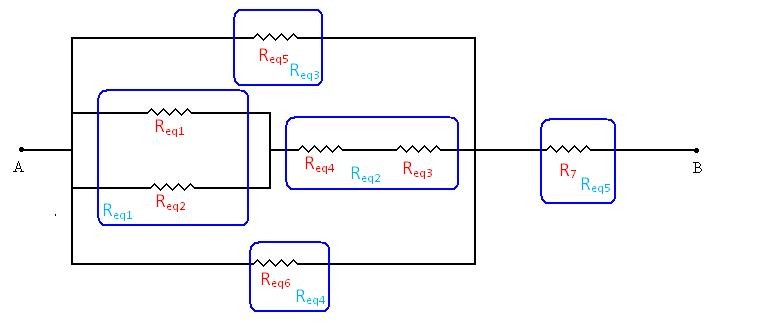Delimitamos agora em azul, para fins de análise, os resistores independentes, e os renomeamos também com azul conforme mostra a Figura 04.

Para cálculo devemos notar agora que há uma associação em paralelo R_eq1, e uma em série R_eq2 .

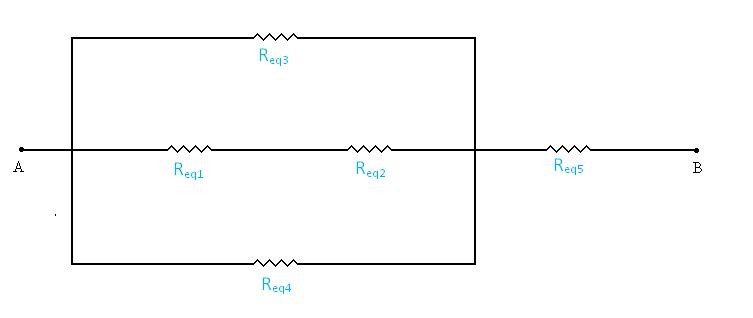
Após efetuar os cálculos obtemos um circuito genérico, mostrado na figura 05.

Após os cálculos teremos: R_eq1 = 100 Ω, R_eq2 = 150 Ω, R_eq3 = 400 Ω, R_eq4 = 400 Ω e R_eq5 = 200 Ω.

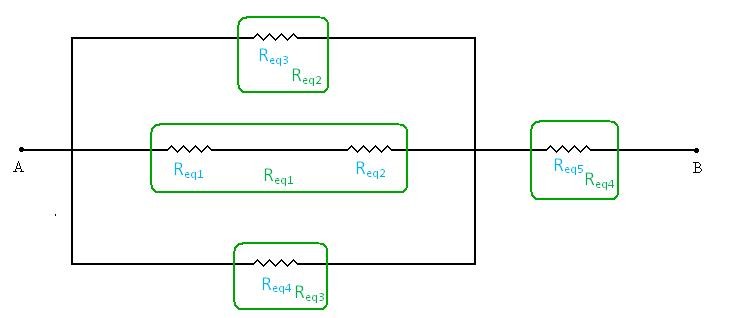Novamente separamos e renomeamos em verde cada resistor ou associação, conforme mostra a figura 06.

Para cálculo devemos notar agora que há uma associação em série R_eq1 .

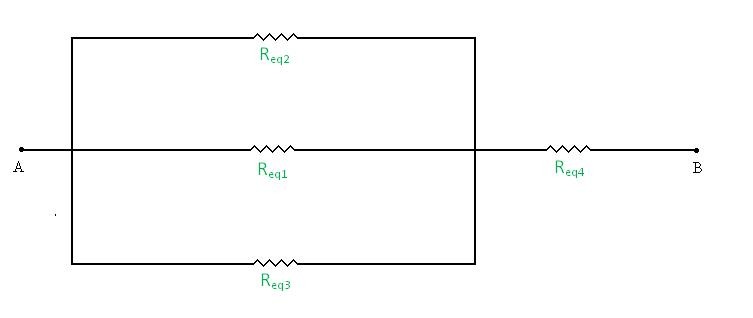Novamente fazemos os cálculos e obtemos o circuito genérico mostrado na figura 07.

Após os cálculos teremos: R_eq1 = 250 Ω.

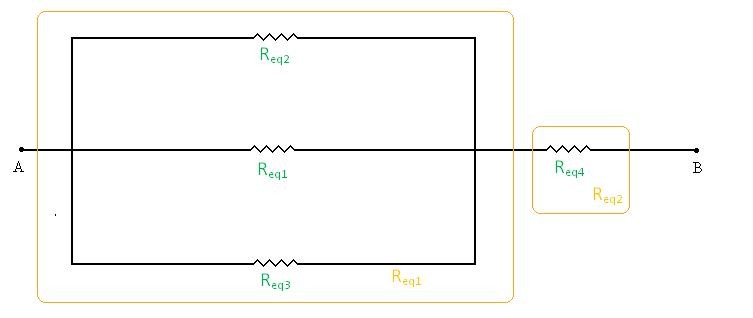Separamos e renomeamos os trechos independentes do circuito em dourado, conforme figura 8.

Para cálculos teremos: R_eq1 = 250 Ω, R_eq2 = 400 Ω, R_eq3 = 400 Ω e R_eq4 = 200 Ω.

Fazemos novamente o cálculo, de modo a obter um circuito equivalente mostrado na figura 9.

Após os cálculos teremos: R_eq1 = 111 Ω e R_eq2 = 200 Ω.

Temos apenas um trecho independente agora. Só pra manter a sequência, delimitaremos agora com cinza e renomearemos, conforme figura 10.

Agora somamos os dois resistores equivalentes.

O resistor equivalente, após os cálculos, é igual ao da figura 11.

Após os cálculos teremos  um único resistor: R_eq1 = 311 Ω.

No link a seguir há exercícios de aplicação: R3 - Exercícios de código de cores e Associação de Resistores.

© Direitos de autor. 2019: Gomes; Sinésio Raimundo. Última atualização: 01/04/2019

Aula 19 - Associação de Resistores em: Série, Paralelo e Misto.

Em um circuito é possível organizar conjuntos de resistores interligados, chamada associação de resistores. O comportamento desta associação varia conforme a ligação entre os resistores, sendo seus possíveis tipos: em série, em paralelo e mista.

1. Associação de resistores em série

Figura 01 - Associação de resistores em série.

Associar resistores em série significa ligá-los de maneira que haja um único trajeto para a passagem da corrente elétrica. Como existe apenas um caminho para a passagem da corrente elétrica esta é a mesma por toda a extensão do circuito. Já a diferença de potencial entre cada resistor irá variar conforme a resistência de cada resistor, é válido a 1ª Lei de Ohm, assim:

• U1 = R1 x I; U2 = R2 x I; U3 = R3 x I e U4 = R4 x I. 

Esta relação também pode ser obtida pela análise do circuito. 

Figura 02 - Divisão de tensão na associação de resistores em série.

Sendo assim a diferença de potencial entre os pontos inicial e final do circuito é igual à:

• U = U1 + U2+ U3 + U4, como:

Esta é a lei das malhas elaborada por kirchhoff.

• U = R1 x I + R2 x I + R3 x I + R4 x I, podemos simplificar: 
• U = (R1 + R2 + R3 + R4) x I.

Analisando esta expressão, já que a tensão total e a intensidade da corrente são mantidas, é possível concluir que a resistência total é:

• RT = R1 + R2 + R3 + R4. 

Um modo de se resumir e lembrar-se das propriedades de um circuito em série é:

• a tensão elétrica (U) se divide;
• a corrente elétrica (i) é a mesma em todos os resistores;
• a resistência total (RT) é a soma algébrica das resistência de cada resistor.

1. Associação de resistores em paralelo

Figura 03 - Associação de resistores em paralelo.

Ligar resistores em paralelo significa basicamente dividir a mesma fonte de corrente, de modo que a tensão elétrica em cada resistor seja a mesma. Usualmente as ligações em paralelo são representadas conforme figura 03.
Como mostra a figura, a intensidade total de corrente do circuito é igual à soma das intensidades medidas sobre cada resistor, ou seja:

• i = i1 + i2 + i3;

Esta é a lei dos nós elaborada por kirchhoff.

Pela 1ª lei de ohm:

• i = (U/R1) + (U/R2) + (U/R3);

E por esta expressão, já que a intensidade da corrente e a tensão são mantidas, podemos concluir que a resistência total em um circuito em paralelo é dada pela soma dos inversos.

Figura 04 - Cálculo de associação de resistores em paralelo.

Um modo de se resumir e lembrar-se das propriedades de um circuito em paralelo é:

• a tensão elétrica (U) nos resistores é a mesma, 
• a corrente elétrica (i) se divide;
• o inverso da resistência total (1/RT) é a soma algébrica do inverso das resistência.

1. Associação de resistores mista

Uma associação mista de resistores consiste em uma combinação, em um mesmo circuito, de associações em série e em paralelo.

Em cada parte do circuito, a tensão (U) e intensidade da corrente serão calculadas com base no que se conhece sobre circuitos série e paralelos, e para facilitar estes cálculos pode-se reduzir ou redesenhar os circuitos, utilizando resistores resultantes para cada parte. No circuito temos R1 em paralelo com R2  e o resistor equivalente R12 em série com R3.

 No link a seguir há exercícios de aplicação: Exercícios de Eletricidade básica.

Nos links a seguir há exercícios de aplicação de associação de resistores: série, paralelo e misto onde temos que utilizar a primeira e segunda lei de Ohm, primeira e segunda lei de Kirchhoff  e lei de Joule: 19_03_01 Associação de resistores , a resolução do terceiro circuito, onde á associação mista de resistores está disponível em: 24_03_03 Associação Mista de Resistores SRG .

No link a seguir há uma Calculadora Científica: Calculadora Científica Online.

© Direitos de autor. 2019: Gomes; Sinésio Raimundo. Última atualização: 22/02/2019

Aula 18 - Gráfico da primeira lei de Ohm

Figura 01 - Circuito elétrico.

Em um circuito elétrico (figura 01), quando a corrente elétrica (i) passa pelo elemento resistivo R, há uma queda de potencial elétrico (u). Essa diferença de potencial decorre do consumo da energia dos elétrons, uma vez que essas partículas transferem parte de sua energia aos átomos da resistência, quando conduzidos por meios que apresentem resistência à sua condução. O fenômeno que explica tal dissipação de energia é chamado de efeito Joule.

A figura 02 mostra o perfil do potencial elétrico antes e após a passagem da corrente por um elemento resistivo de um circuito elétrico, observe a queda de energia. Quando a corrente elétrica é conduzida em um corpo com resistência elétrica, parte de sua energia é dissipada em forma de calor.

Figura 02 - Queda de potencial elétrico.

A corrente elétrica i mede o fluxo de cargas pelo corpo em Ampères (ou em C/s). A corrente elétrica é inversamente proporcional à resistência elétrica dos corpos: quanto maior a resistência elétrica de um corpo, menor será a corrente elétrica a atravessá-lo.

A figura 03 mostra o gráfico da primeira lei de Ohm.

Para construirmos o gráfico U x I, usamos a fórmula da primeira lei de Ohm: R = U x i [Ohm].

Figura 03 - Gráfico U x i.

Escolheremos valores aleatórios para U e i e os anotaremos na tabela abaixo.

U (V) 0 3 6 9

i (A) 0 2 4 6

Depois, marcaremos o par ordenado para em seguida ligar todos os pontos e encontrarmos o gráfico, que nesse caso se trata de uma reta inclinada que representa a resistência elétrica, conforme gráfico de um resistor ôhmico, mostrado na figura 03.

Podemos encontrar o valor da resistência por meio do gráfico de duas formas distintas. A primeira é substituindo os valores da diferença de potencial (U) e da corrente na fórmula da primeira lei de Ohm. Já a segunda é encontrando o valor da tangente de θ (ângulo de inclinação da reta).

Chamamos de resistor ôhmico todo corpo capaz de apresentar resistência elétrica constante para um determinado intervalo de tensões elétricas. O gráfico de tensão em função da corrente elétrica para os resistores ôhmicos é linear, como mostra a figura 03.

O resistor pode ser considerado ôhmico no intervalo em que o seu potencial elétrico aumenta linearmente com a corrente elétrica.

Figura 04 - Tangente do gráfico U x i.

Tomando-se o segmento reto do gráfico, sabe-se que o potencial elétrico entre os terminais de um resistor sofrerá uma variação em seu potencial elétrico que é sempre proporcional à corrente elétrica que o percorre.

Analisando o gráfico mostrado acima, vemos que a resistência elétrica pode ser entendida como a inclinação da reta, dada pela tangente do ângulo θ. Como sabemos, a tangente é definida como a razão entre os catetos oposto e adjacente e, portanto, pode ser calculada com a fórmula R = U/i, no caso em que as resistências são ôhmicas.

R = tan θ

R = tan 30°

R = 3√3 Ω

No link a seguir há exercícios de aplicação de para: Elaboração do Gráfico V x I ( Primeira Lei de Ohms),elaborado pelo Prof. Sinésio Raimundo Gomes: 24_03_02 R2_Gráfico_Lei_de_Ohm_SRG e o resultado pode ser verificado em: 24_03_02 R2R_Gráfico_Lei_de_Ohm_SRG .

© Direitos de autor. 2019: Gomes; Sinésio Raimundo. Última atualização: 22/02/2019

Aula 17 - Formas construtivas, valores comerciais e código de cores de Resistores

Figura 01 - Forma construtiva de resistores.

A resistência é diretamente proporcional ao comprimento e à resistividade do material , e inversamente proporcional à área da secção transversal. 

A equação para determinar a resistência de uma seção do material é: 
Onde:  P (letra grega "rô') é a resistividade do material,  L o comprimento e A a  área da secção transversal.

Fabricação: A matéria prima para fabricação deste resistor é a base cerâmica revestidas com óxido de metal, (condutor elétrico). A resistência elétrica é formado depois com o resultado da modificação de óxido de metal sobre a superfície da base cerâmica. Em seguida é realizado o fechamento da base cerâmica a fim de que a extremidade do resistor pode ser soldada ao fio. 

Figura 02 - Código de cores de resistores.

É realizado uma incisão em espiral sobre a camada da superfície de óxido de metal da base, que criara uma ranhura em espiral, para determinar o valor da resistência (ohms) com precisão com uma certa tolerância. 

Quanto maior o valor da resistência a ser alcançado maior será o corte (incisão), após esta etapa são soldados os terminais  e é realizado revestimento e impressão do valor ou o código de cores do resistor no corpo. Todos os resistores são colados em uma de fita em ambas as extremidades do resistor para facilitar a contagem e embalagem. A contagem e embalagem é o processo final antes do envio para o cliente.

A função do resistor é limitar o fluxo de corrente elétrica. Este símbolo é usado para indicar um resistor em um diagrama de circuito, conhecido como um diagrama esquemático.

Valor da resistência é designada em unidades chamadas de "Ohm." Um resistor de 1000 é geralmente mostrado como 1K Ohm (kilo Ohm) e 1000 K-Ohms é escrito como 1M Ohm (megohm).
Há duas classes de resistores; resistores fixos e os resistores variáveis. 
Eles são também classificados de acordo com o material de que são feitos. O resistor típico é feito de película ou filme de carbono ou metálico, que reveste seu corpo cerâmico.
O valor da resistência não é a única coisa a  considerar quando se selecciona um resistor para utilização num circuito. A "tolerância" e a potência do resistor também são importantes.
A tolerância de um resistor denota o quão próximo está o valor real de resistência nominal. Por exemplo, uma tolerância de ± 5%, indicaria uma resistência que está dentro de ± 5% do valor da resistência especificada.

Figura 03 - Tamanho de resistores em razão de sua potência.

A potência indica o quanto de energia o resistor pode tolerar sem queimar. A potência máxima nominal da resistência é especificada em Watts. Potência é calculado com o quadrado da corrente (I2) x o valor da resistência (R) do resistor. Se é utilizado em sua máxima potência, torna-se extremamente quente, quando trabalhamos com metade de sua potência, o resistor trabalha morno. e com 1/3 trabalha frio. O tamanho físico das resistências diferentes têm relação com a potência do resistor.
Resistores em circuitos eletrônicos são tipicamente de 1/8W, 1/4W, e 1/2W. Ao ligar um diodo emissor de luz (LED), há um fluxo relativamente grande corrente através do resistor, então você precisa considerar a potência do resistor que você escolher.
Valor da resistência: Quanto ao valor da resistência padrão, os valores utilizados podem ser divididos como um logaritmo. No caso de E24: [1.0], [1.1], [1.2] ,[1.3], [1.5],[1.6], [1.8], [2.0], [2.2], [2.4], [2.7], [3.0], [3.3], [3.6], [3.9], [4.3], [4.7], [5.1], [5.6], [6.2], [6.8], [7.5],[8.2], [9.1] totalizando 24 valores comerciais e seus múltiplos: x 0,01; x 0,1; x 1; x 10; x 100; x 1000; x 10.000; x 100.000; x 1.000.000.
O valor da resistência é exibido usando o código de cores (as barras coloridas / as faixas coloridas), porque a resistência média é muito pequena para ter o valor impresso nela com números.
No multímetro analógico antes de tudo é necessário realizar uma calibração. Para isto: Escolha a escala a ser utilizada; Coloque as duas pontas de prova do Multímetro em contato e através do potenciômetro de calibração ajusto para zero;  Desfaça o contato das pontas e realize o teste.

Os multímetros analógicos possuem uma escala começando do zero (direita) e terminando na esquerda. Estas escalas são múltiplos de 10 que devem ser multiplicadas pelo valor que o ponteiro apontar durante a medição. O componente a ser medido não pode estar ligado ao circuito e nem submetido a qualquer tensão. Para medir, ligamos as pontas de prova do multímetro em paralelo com os terminais do resistor.

Informações sobre Resistores de filme de carbono podem ser obtidas no link: 19_05_01 Resistor de Filme de carbono.

Informações sobre Resistores de filme metálico podem ser obtidas no link: 19_05_01 Resistor de Filme Metálico.

Informações sobre Resistores de fio metálico podem ser obtidas no link: 19_05_01 Resistor de Fio Metálico.

Informações sobre Resistores cerâmicos podem ser obtidas no link: 21_04_01 Resistor Cerâmico.

A folha de dados com o código de cores de resistores da série E24 de 4 anéis pode ser obtidas no link: 20_07_01 Código de cores de Resistor.

Há no link á seguir um resumo de informações sobre resistores elaborado pelo Prof. Sinésio Raimundo Gomes que pode ser baixada em: 23_04_01 Tudo sobre Resistores SRG.

No link a seguir há exercícios de aplicação de para: Identificação (cores dos anéis), decodificação (valor nominal), cálculo (resistência mínima e máxima tolerável) e verificação (valor real), elaborado pelo Prof. Sinésio Raimundo Gomes: 24_03_01 - Identificação e decodificação código de resistores SRG.

No link a seguir há uma calculadora para código de cores de resistores: Calculadora para código de cores de resistores.

© Direitos de autor. 2019: Gomes; Sinésio Raimundo. Última atualização: 15/03/2024